Publications

MeshfreeFlowNet: A Physics-Constrained Deep Continuous Space-Time Super-Resolution Framework

ACM/IEEE Supercomputing Conference 2020 - Finalist for Best Student Paper Award

Authors - Chiyu “Max” Jiang*, Soheil Esmaeilzadeh*, Kamyar Azizzadenesheli, Karthik Kashinath, Mustafa Mustafa, Hamdi A. Tchelepi, Philip Marcus, Prabhat, and Anima Anandkumar

*denotes equal contribution

Download the Paper Code Repository

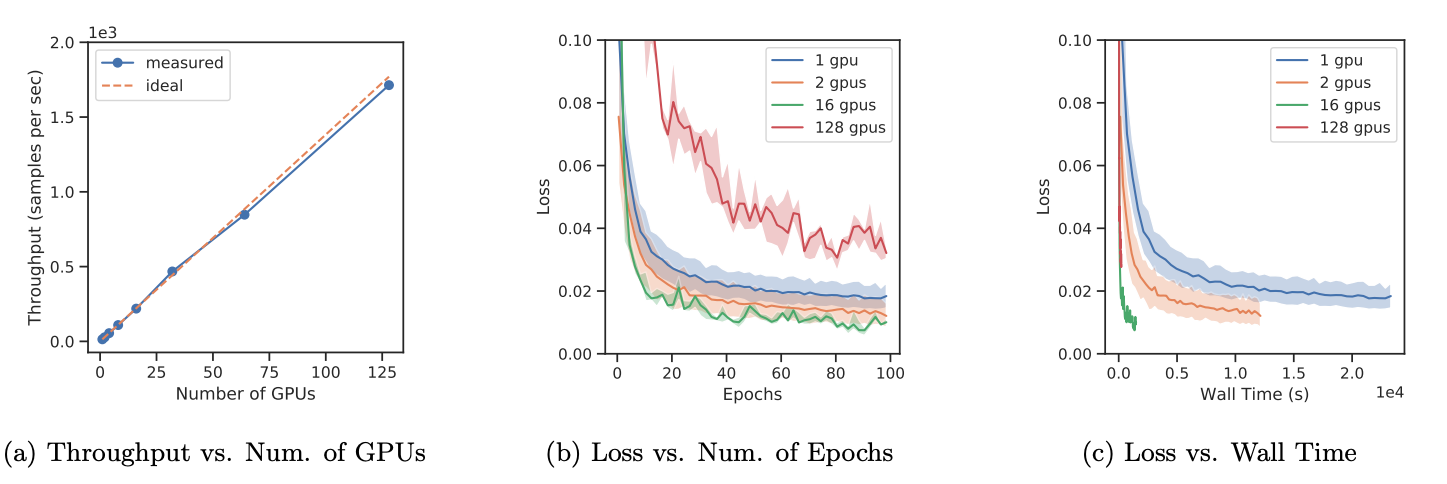
Abstract - We propose MeshfreeFlowNet, a novel deep learning-based super-resolution framework to generate continuous (grid-free) spatio-temporal solutions from the low-resolution inputs. While being computationally efficient, MeshfreeFlowNet accurately recovers the fine-scale quantities of interest. MeshfreeFlowNet allows for (i) the output to be sampled at all spatio-temporal resolutions, (ii) a set of Partial Differential Equation (PDE) constraints to be imposed, and (iii) training on fixed-size inputs on arbitrarily sized spatio-temporal domains owing to its fully convolutional encoder. We empirically study the performance of MeshfreeFlowNet on the task of super-resolution of turbulent flows in the Rayleigh–Bénard convection problem. Across a diverse set of evaluation metrics, we show that MeshfreeFlowNet significantly outperforms existing baselines. Furthermore, we provide a large scale implementation of MeshfreeFlowNet and show that it efficiently scales across large clusters, achieving 96.80% scaling efficiency on up to 128 GPUs and a training time of less than 4 minutes. We provide an open-source implementation of our method that supports arbitrary combinations of PDE constraints

Keywords: Super-Resolution, PDEs, Physics-Constrained, Deep Neural Networks


MeshfreeFlowNet: a novel deep learning-based super-resolution framework to generate continuous (grid-free) spatio-temporal solutions from the low-resolution inputs.

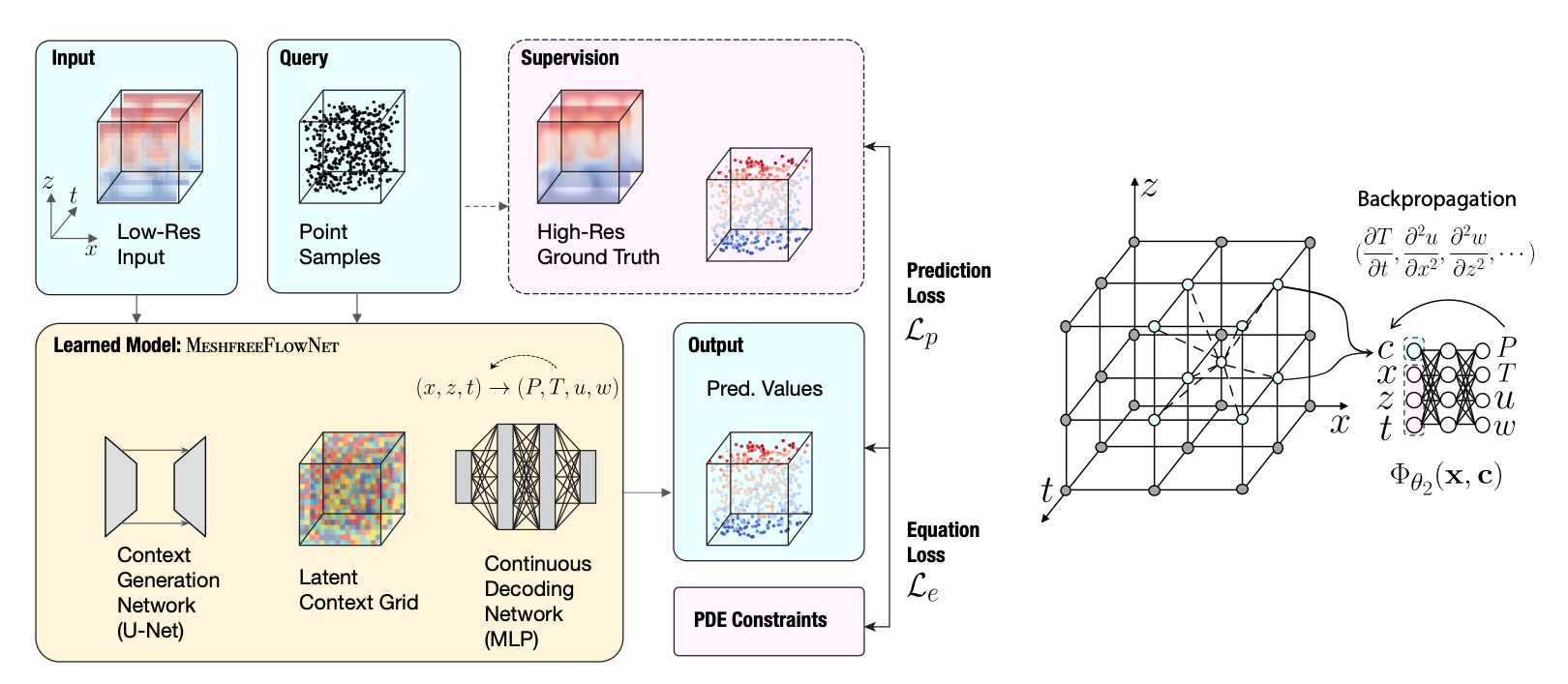
alternate text

Sample tuples of the ground truth high-resolution data, the low-resolution input data for MeshfreeFlowNet, and the high-resolution super-resolved data by MeshfreeFlowNet for the 4 physical parameters of the Rayleigh–Bénard problem namely $T$, $p$, $u$, $w$ as the temperature, pressure, and the x and z components of the velocity.

Highlights

alternate text


Fig.1. Schematic for the training pipeline for MeshfreeFlowNet model for continuous space-time super-resolution. An input low-resolution grid is fed to the Context Generation Network that creates a Latent Context Grid. A random set of points in the corresponding space-time domain is sampled to query the Latent Context Grid, and the physical output values at these query locations can be continuously decoded using a Continuous Decoding Network, implemented as a Multilayer Perception. Due to the differentiable nature of the MLP, any partial derivatives of the output physical quantities with respect to the input space-time coordinates can be effectively computed via backpropagation, that can be combined with the PDE constraints to produce an Equation Loss. On the other hand, the predicted value can be contrasted with the ground truth value at these locations produced by interpolating the high-resolution ground truth to produce a Prediction Loss. Gradients from the combined losses can be backpropagated to the network for training.

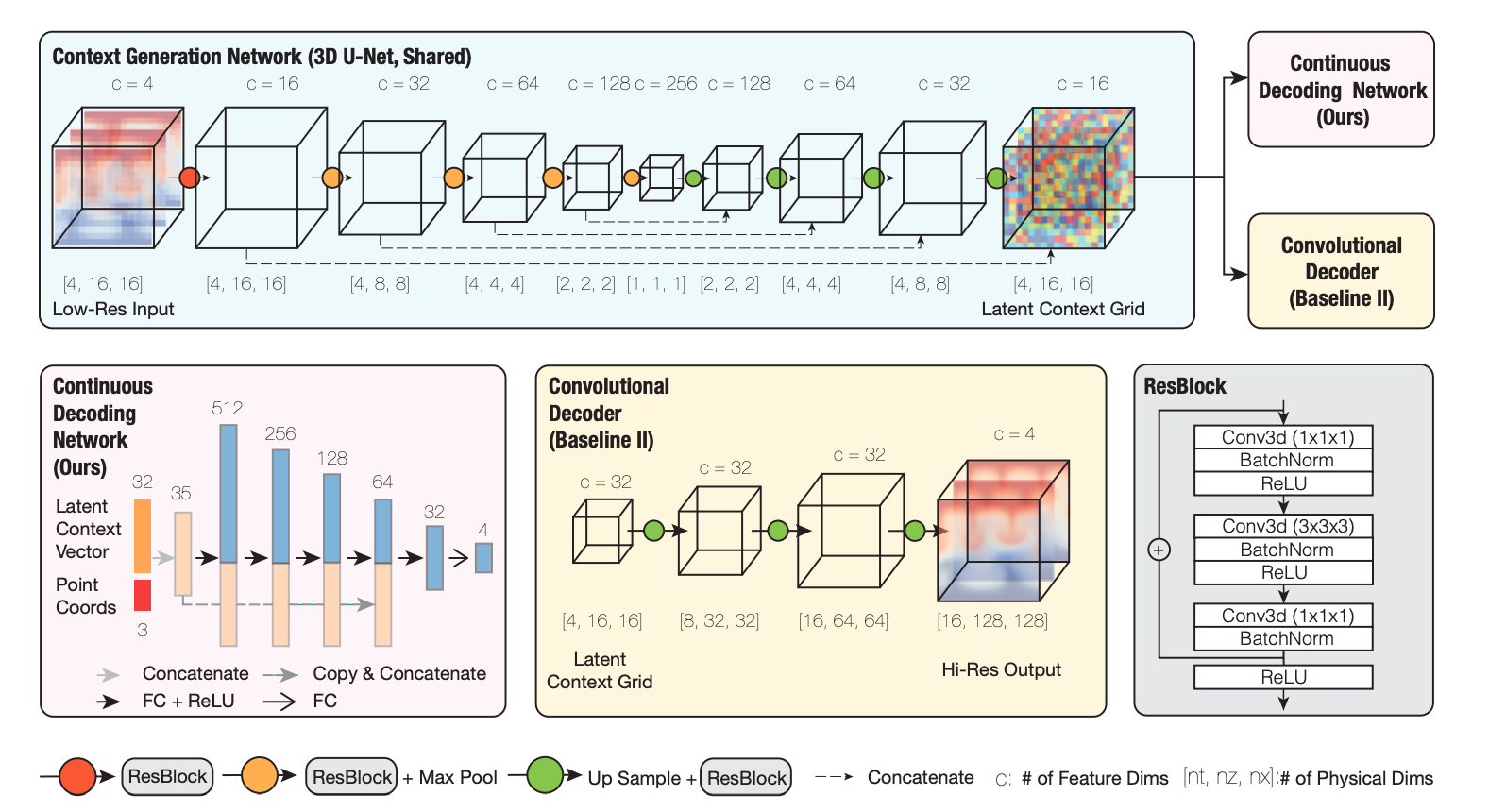
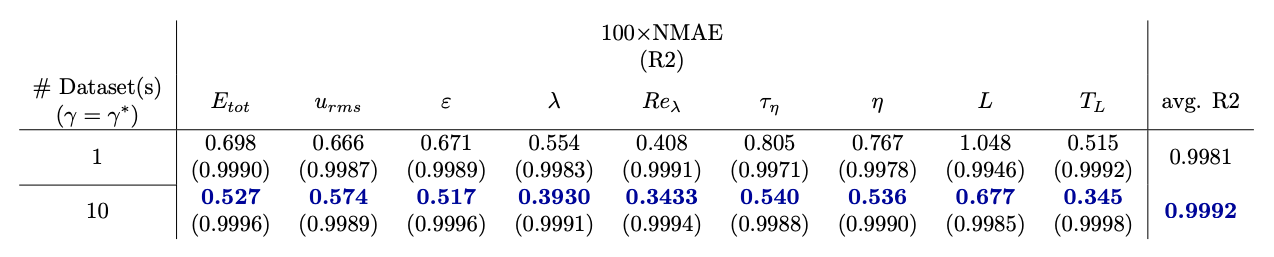
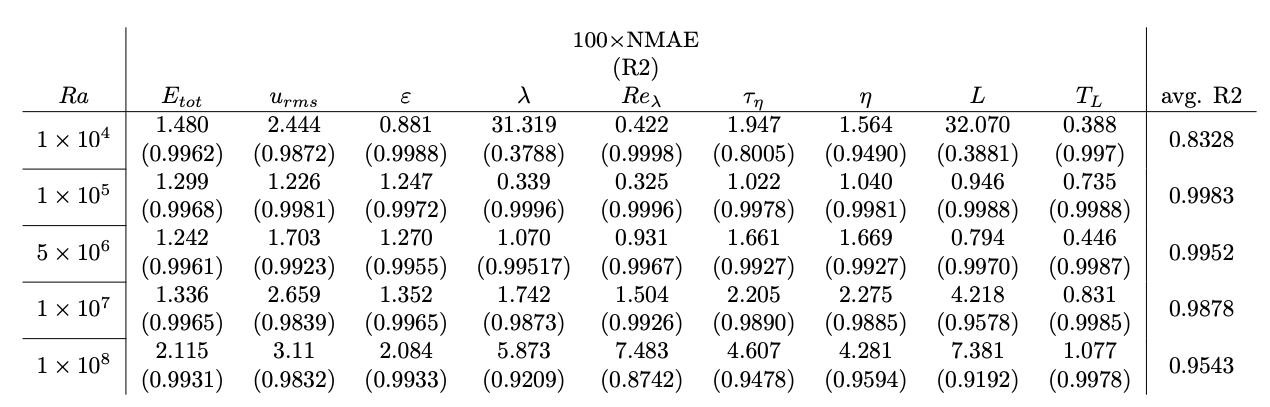
alternate text

Fig.2. A schematic for the architecture of the MeshfreeFlowNet framework. MeshfreeFlowNet consists of two end-to-end trainable modules: the Context Generation Network, and the Continuous Decoding Network. The Baseline (II) method that we exhaustively compare with share the same 3D U-Net structure in the encoding arm, but instead uses a convolutional decoder for producing the final output. In comparison, the MeshfreeFlowNet allows for continuous output that can be sampled at arbitrary space-time locations.

alternate text

Fig.3. Comparison between the performance of MeshfreeFlowNet framework for super-resolving the low-resolution data vs. two baseline models.

alternate text

Fig.4. For a MeshfreeFlowNet model that has been respectively trained on 1 dataset and 10 datasets each having a different initial condition, the super-resolution performance evaluation is reported on a dataset with an unseen initial condition.

alternate text

Fig.5. For a MeshfreeFlowNet model that has been trained on 10 datasets each having a different boundary condition (Rayleigh number) as Ra ∈ [2, 90] × 105 with Pr = 1, the super-resolution performance evaluation is reported for: a Rayleigh number within the range of boundary conditions of the training sets (i.e., Ra = 5×106), Rayleigh numbers slightly below and above the range of boundary conditions of the training sets (i.e., Ra = 1 × 105 and Ra = 1 × 107 respectively), and Rayleigh numbers far below and above the range of boundary conditions of the training sets (i.e., Ra = 1 × 104 and Ra = 1 × 108 respectively).

alternate text

Fig.6. Scaling performance on up to 128 GPUs on NERSC Cori GPU cluster. Scaling efficiency is close to ideal performance, at 96% with all 128 GPUs. Training convergence is greatly accelerated by scaling across more GPUs. The shaded band in Figs. (b)-(c) denotes the (10%, 90%) noise interval. Throughput refers to the number of samples per second.
Tags: