Active Cloaking in Stokes Flows via Reinforcement Learning

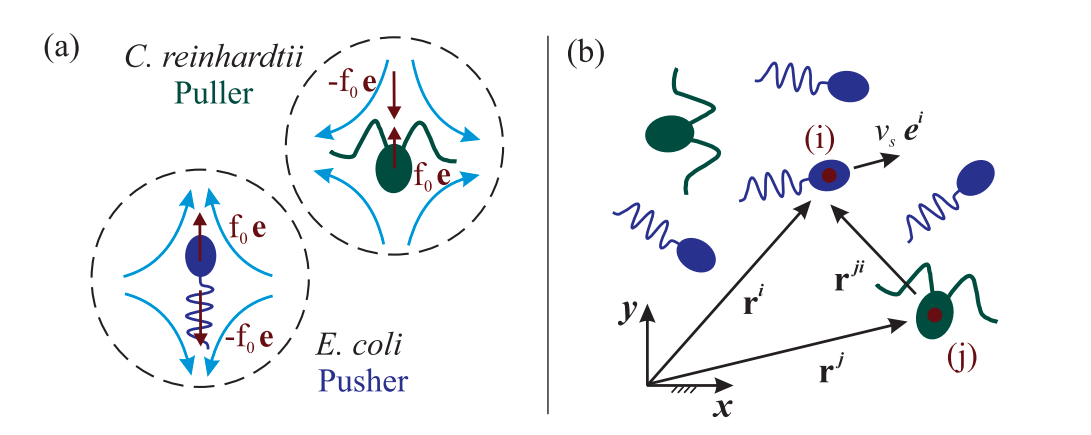
Fig.1. (a) Schematic representation of the archetypal puller and pusher swimmers. The force dipole ($\pm f_0\mathbf{e}$) exerted by each swimmer to the surrounding fluid is shown by red arrows. Vector $\mathbf{e}$ denotes the swimming direction, and curly blue arrows demonstrate direction of the induced disturbing flows in each case. (b) Schematic representation for a system of interacting micro-swimmers. The position vector of swimmer $i \in \lbrace 1...N \rbrace$, swimming with speed $V_s$ in direction $\mathbf{e}^i$, is denoted by $\mathbf{r}^i$ with respect to the fixed frame of reference. As a benchmark, here the presented system includes $N = 6$ swimmers of pusher and puller types.

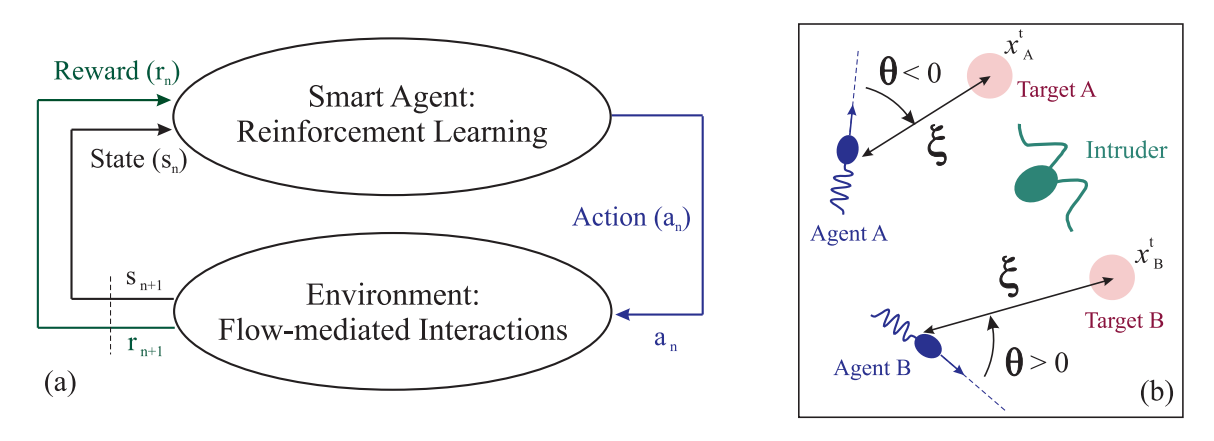
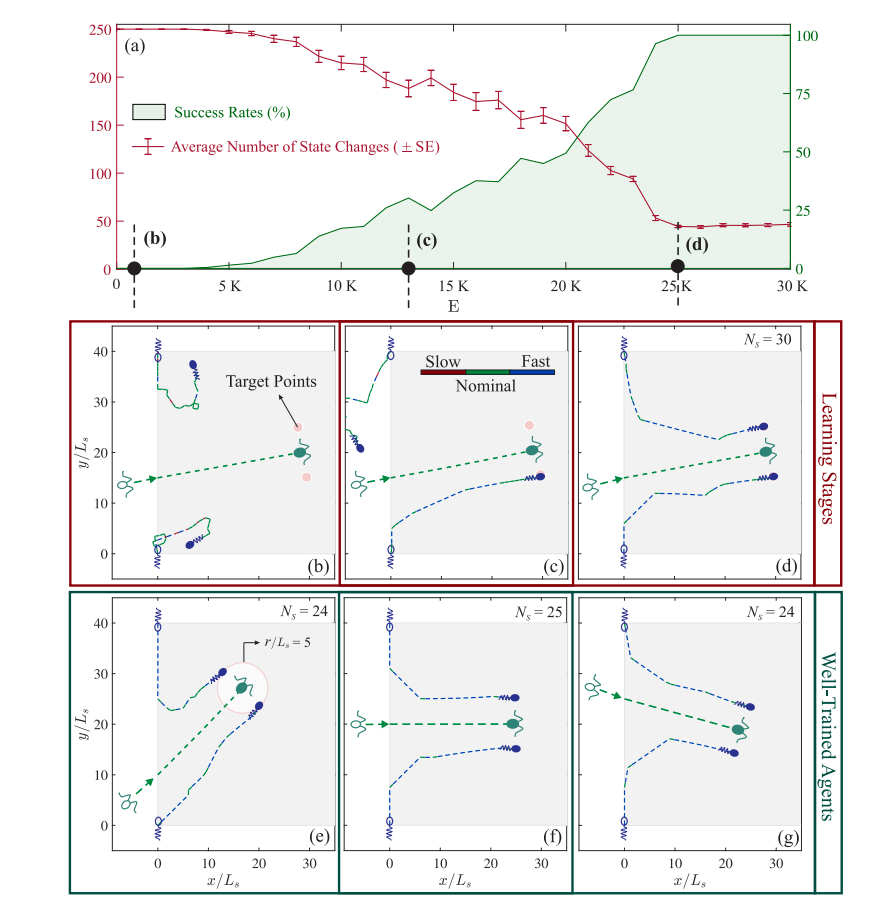
Fig.3. (a) The learning process is assessed in terms of the agent’s success rate, and number of the required swimming actions. After every 1000 training episodes, a set of 100 random active-cloaking tests have been performed using a purely deterministic policy based on the most updated $Q$-matrix at the moment. Each of the testing episodes starts with an intruder randomly entering a guarded region (shaded in gray; see panels b-g) from a random position and swimming toward a random direction, while the cloaking agents are initially positioned on the sides of entrance (see e.g. panels b-g). The test results are presented throughout the learning phase in terms of: (i) the success rate (shown in green) of the agents in catching the intruders and forming the desired active cloak, as well as (ii) the number of total state-changes (average ± Standard Error) in each set of testing episode (shown in red). (b)-(d) Benchmarks of different learning stages. The panels represent a sample test on realizing an active cloak around a random intruder, performed in three different learning stages, i.e. non-adaptive (b), intermediate-adaptive (c), and well-adaptive (d) stages. The episode number ($E$) corresponding to each of the panels (b-d) is marked in panel (a), and agents use the most updated behavioral policy at each stage. The intruder (here a puller shown in green) and the cloaking agents (pushers shown in blue) are also represented both at the initial and final positions with stripe and solid schematics, respectively. Trajectories of the swimmers are shown in each panel by dashed lines, and color-coded based on the swimming speed at the moment – see the legend in panel (c). The assigned target points (to realize the desired symmetrical active cloak) for each of the agents is also marked in each panel (pink markers). (e)-(g) Sample tests performed using well-trained cloaking agents, equipped with welladaptive behavioral policy, which is obtained after convergence of the success rate to 100% (see panel a). The number of required swimming actions (or equivalently the number of state-changes, $N_s$) is denoted on each panel. At this stage, the agents are capable of identifying the fastest non-invasive paths toward forming the desired active cloak around any randomly moving intruder. The target arrangement here is to symmetrically position on the sides of intruder, with a separation distance $r_0/L_s = 5$ (see e.g. panel e). The learning hyper-parameters are set to $\alpha = 0.3$, $\gamma = 0.95$, and $\varepsilon = 0.01$.

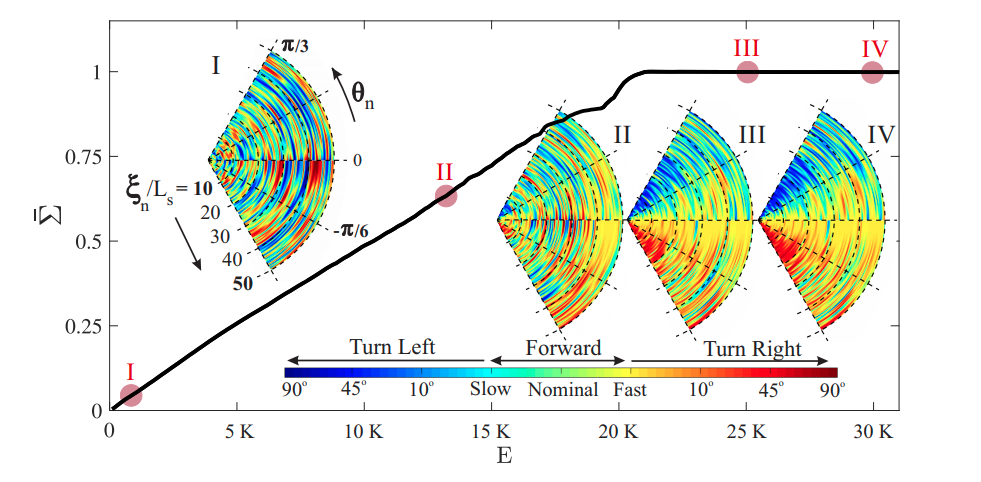
Fig.4. Evolution of the normalized, element-wise sum of the $Q$-matrix ($\bar{\Sigma}$) through successive training episodes ($E$) during the learning phase. Evolution of the behavioral policy is also visualized (see insets I-IV) by color-coding over a selected sector of the state-space at four different learning stages (marked over the curve by I-IV), which eventually converges to the optimal action policy. Each swimming action is presented by a color-code (see the color-bar legend), and every point in the statespace is shaded by the color representing swimmers’ understanding of the best action at that specific state. The training episodes are the same as those presented in Fig. 3, for which the learning hyperparameters are set to $\alpha = 0.3$, $\gamma = 0.95$, and $\varepsilon = 0.01$.

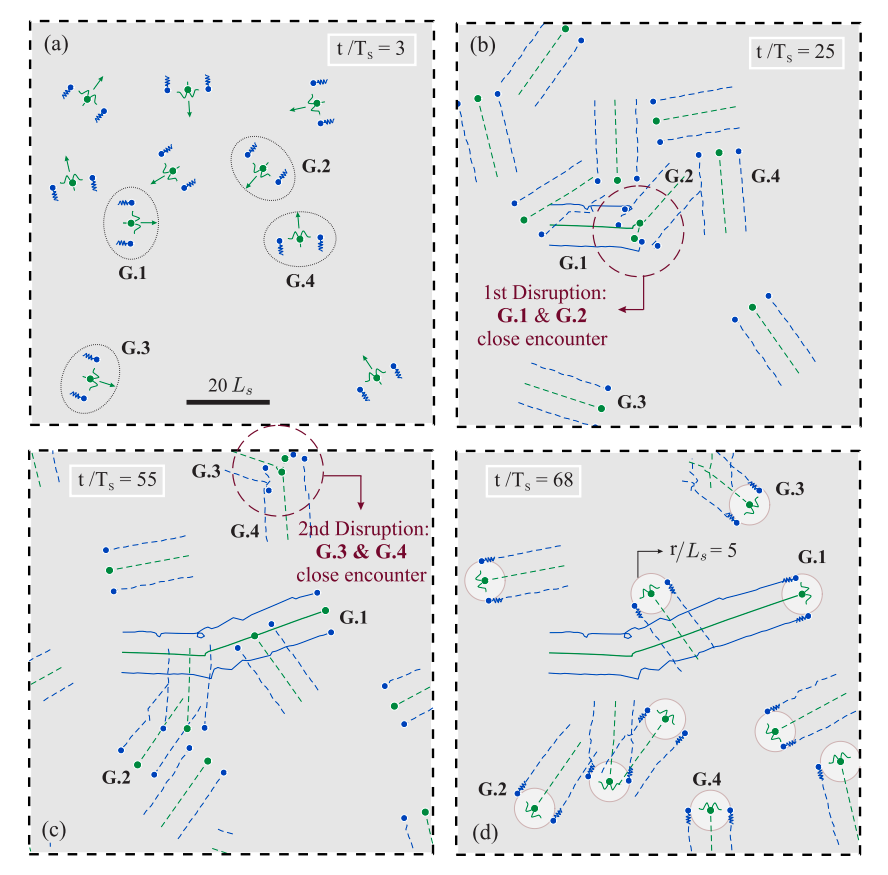
Fig.5. Time evolution of a crowded suspension of intruders (shown in green), each of which actively cloaked by a pair of smart micro-swimmers (shown in blue). Here the intruders are freely moving toward random directions in space – specified by green arrows in (a). Periodic boundary conditions are imposed on the presented panels – i.e. each panel represents just a window of an infinite domain at that specific moment. As demonstrated through snapshots (a)-(d) of the system’s time evolution (see also Movie S1), using their adaptive decision-making intelligence, our agents are able to robustly maintain the cloak formation in the presence of complex hydrodynamic interactions. They are also able to immediately restore the desired formation after any sever close encounters (b-c) which cause major disruptions to the cloak. As a benchmark, the evolution dynamics of four sample groups (G.1-4) are tracked in the panels. Specifically, the close encounter between G.1 & G.2 as well as G.3 & G.4 are marked by red dashed circles in panels (b) and (c), respectively. Also, trajectories of the swimmers in G.1 are shown by solid lines throughout the time, while other groups’ trajectories are only demonstrated (by dashed lines) within the last 25$T_s$ of their motion. The time corresponding to each snapshot is noted in each panel, and swimmer schematics are added to panels (a) and (d) for readability. Here, the goal was to realize an active version of the symmetric cloak presented in Fig. 2. Thus, for the reference, rings of radii $r/L_s = 5$ (that is equal to the predefined desired separation distances) are depicted around intruders in the final snapshot (d).

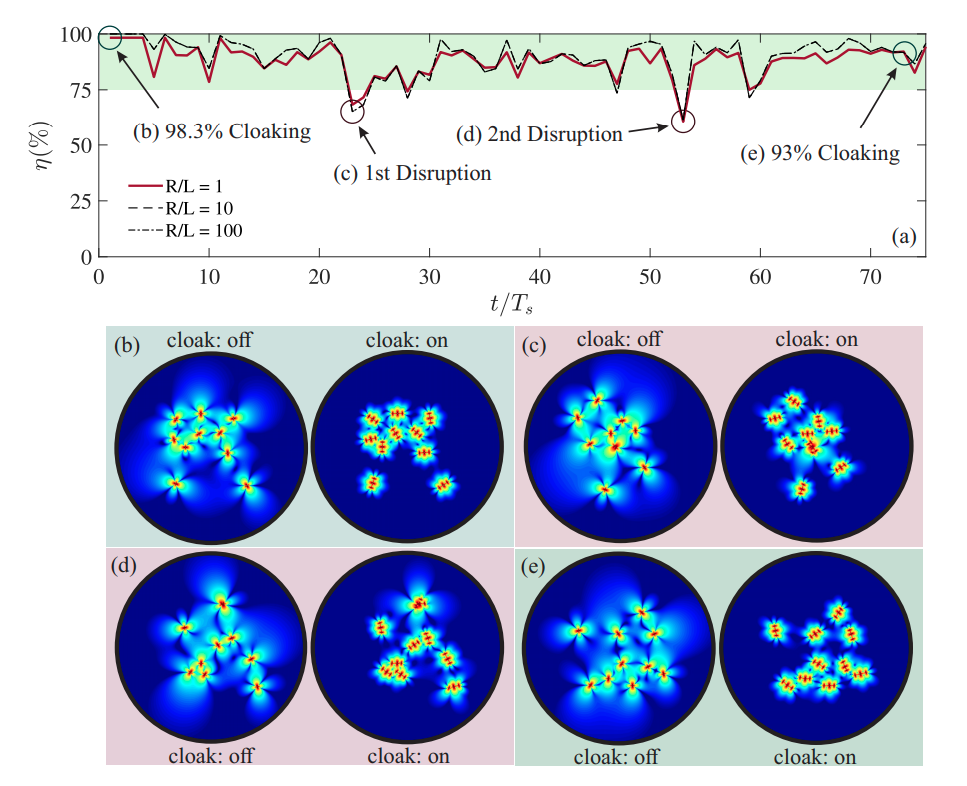
Fig.6. (a) Time evolution of the overall cloaking performance ($\eta$ %) corresponding to the flock of smart micro-swimmers deployed within the crowded suspension presented in Fig. 5 to cloak random intruders. Here $\eta$ (%) is monitored over the entire time evolution at ranges $R/L = 1$ (red solid line), $R/L = 10$ (black dashed line), and $R/L = 100$ (black dash-dotted line), where $L$ is the length of each presented window in Fig. 6. ($\mathbf{b}$-$\mathbf{e}$) Snapshots of the induced fluid disturbances are visualized (by color shading) over the entire system (cloak: on), and also compared to those induced when no cloaking agents are deployed (cloak: off). The moment corresponding to each of the snapshots in (b-e) is marked on the curve in (a). Specifically, we demonstrate the snapshots at: (i) an early stage, where the desired cloaks ($\eta \approx 98$%) have been just formed (Figs. 5a, 6b); (ii) the moments of close encounters happening between G.1 & G.2 (1st Disruption, see Figs. 5b, 6c) as well as G.3 & G.4 (2nd Disruption, see Figs. 5c, 6d), respectively, where the implemented cloaks undergo sever disruptions; and (iii) a final recovered stage (Figs. 5d, 6e) where the agents are once again perfectly in the desired cloaking arrangements ($\eta \approx 93$%).