Authors - Soheil Esmaeilzadeh, Zhipeng Qin, Amir Riaz, and Hamdi A. Tchelepi
Download the Journal Version
Abstract - We study the interfacial evolution of immiscible two-phase flow within a capillary tube in the partial wetting regime using direct numerical simulation. We investigate the flow patterns resulting from the displacement of a more viscous fluid by a less viscous one under a wide range of wettability conditions. We find that beyond a wettability dependent critical capillary number, a uniform displacement by a less viscous fluid can transition into a growing finger that eventually breaks up into discrete blobs by a series of pinch-off events for both wetting and nonwetting contact angles. This study validates previous experimental observations of pinch-off for wetting contact angles and extends those to nonwetting contact angles. We find that the blob length increases with the capillary number. We observe that the time between consecutive pinch-off events decreases with the capillary number and is greater for more wetting conditions in the displaced phase. We further show that the blob separation distance as a function of the difference between the inlet velocity and the contact line speed collapses into two monotonically decreasing curves for wetting and nonwetting contact angles. For the phase separation in the form of pinch-off, this work provides a quantitative study of the emerging length and timescales and their dependence on the wettability conditions, capillary effects, and viscous forces.
Keywords: Displacement of immiscible fluids, Microfluidics, Porous media, Wetting
Highlights 
Fig.1. A capillary tube is illustrated in an axisymmetric computational domain where $z$ and $r$ are the axial and radial coordinates, respectively. The axis of symmetry is represented by $OO'$, $AB$ is the solid wall boundary, and $OA$ and $O'B$ are respectively the inlet and outlet boundaries. The interface is shown in red with the level-set function $\phi =0$ at the interface and $\phi>0$ and $\phi<0$ in the advancing and receding fluid phases with respective density and dynamic viscosity of $\rho_1, \mu_1$ and $\rho_2,\mu_2$. $\mathbf{n}$ represents the interface normal vector. $\theta$ is the interface contact angle at the triple point where the interface is in contact with the solid wall boundary. $L_t$, $R$, $D$ are respectively the length, radius, and diameter of the capillary tube. Throughout this work we consider a tube length to diameter ratio of $L_t/D = 10$ with $D= 0.00073\,[m]$.
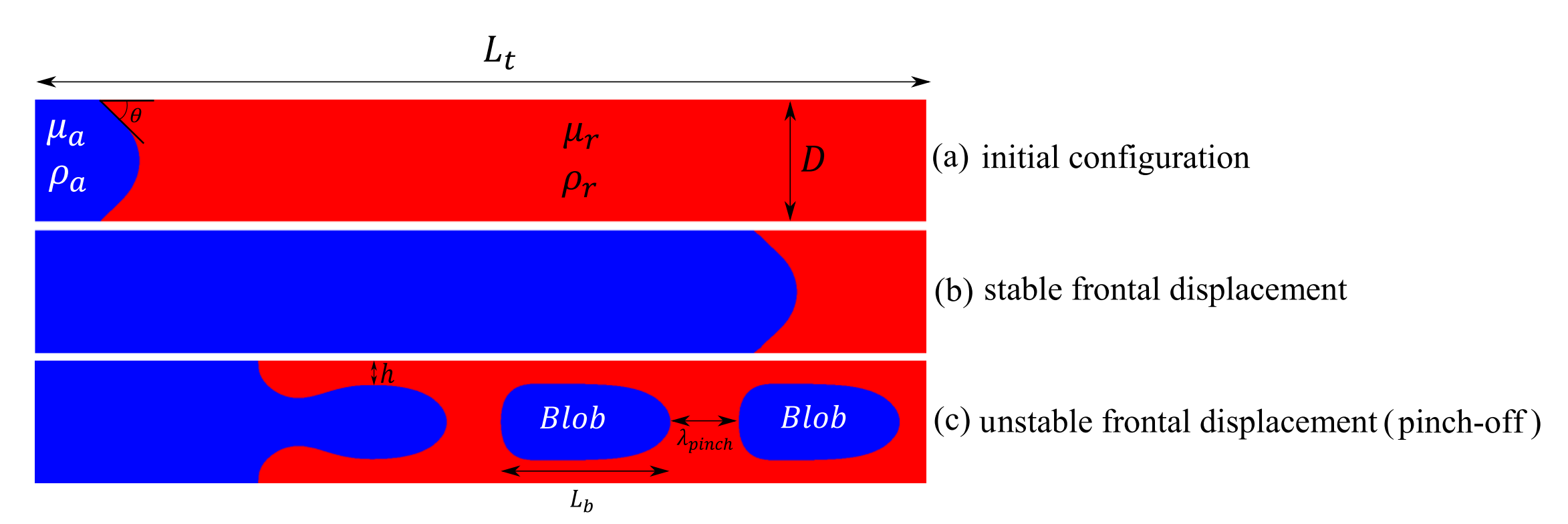Fig.2. (a) The initial state of the immiscible two-phase flow within the capillary tube of diameter $D$ and length $L_t$ with $L_t/D = 10$ and $D = 0.00073\,[m]$. $\mu_a, \rho_a$ and $\mu_r, \rho_r$ are dynamic viscosity and density of the advancing and receding phases, respectively. (b) The stable frontal displacement where the advancing phase moves at a constant speed corresponding to the injection flow rate. (c) The unstable frontal displacement where the advancing fluid transitions into a finger that leaves a layer of the receding phase (with thickness $h$) on the wall. Eventually, the finger breaks up into blobs due to the pinch-off phenomenon. The blobs have a length of $L_b$ and a separation distance of $\lambda_{pinch}$.
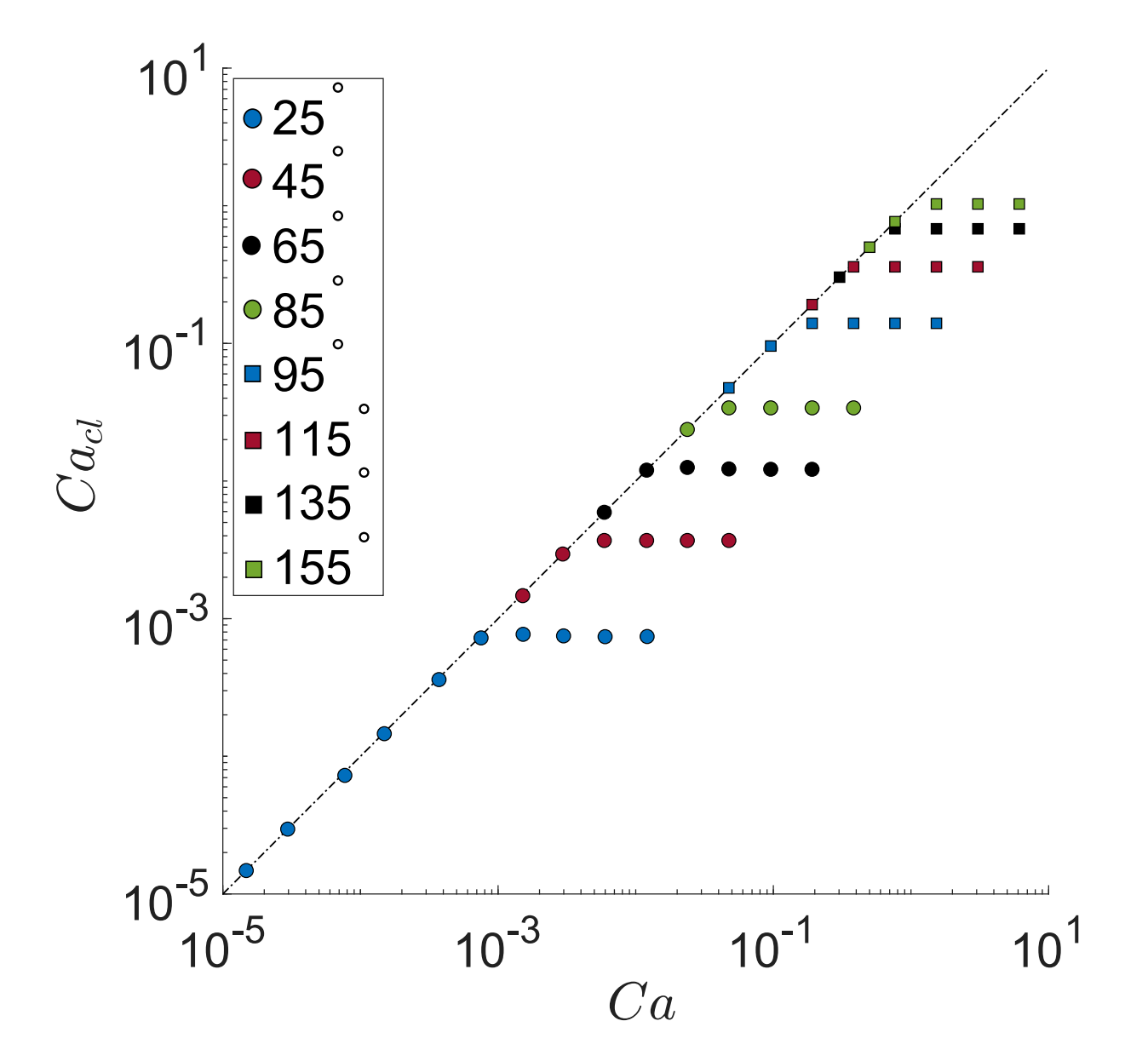Fig.3. Illustration of the contact line capillary number ($\text{Ca}_{cl}$) as a function of the injection capillary number ($\text{Ca}$) for wetting ($\theta<90^\circ$) and non-wetting ($\theta>90^\circ$) contact angles. The contact line capillary number is defined as $\text{Ca}_{cl} = \mu_r u_{cl}/\sigma$ where $u_{cl}$ is the speed of the contact line. The injection capillary number is defined as $\text{Ca} = \mu_r u_{in}/\sigma$ where $u_{in} = 4Q_{in}/(\pi D^2)$ is the inlet velocity corresponding to the injection flow rate ($Q_{in}$)
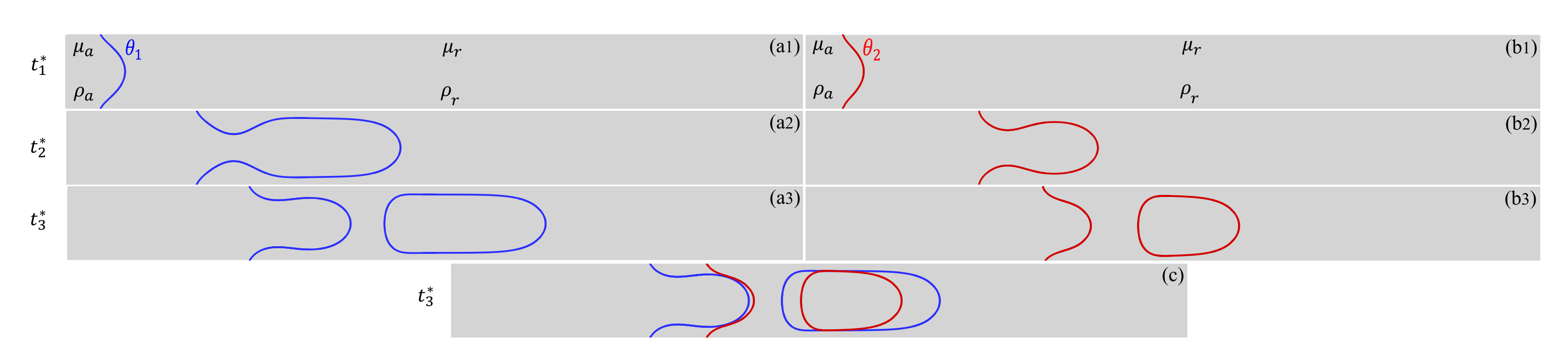Fig.4. Plots (a1) to (a3) and (b1) to (b3) show the interfacial evolution at three different time frames, $t^*_1$ to $t^*_3$, respectively for two wetting contact angles, $\theta_2 = 85^\circ > \theta_1 = 75^\circ$. For both contact angles, the capillary number ($\text{Ca}$) is the same, and above their corresponding critical contact line capillary numbers. ($\mu_a, \rho_a)$, $(\mu_r, \rho_r)$ are dynamic viscosity and density of the advancing and receding phases, respectively. Plot (c) compares the interfaces for contact angles $\theta_1 = 75^\circ$ and $\theta_2 = 85^\circ$ at the time frame $t^*_3$ shown in plots (a3) and (b3), where the interface corresponding to the contact angle $\theta_2 = 85^\circ$ is ahead of the interface corresponding to the smaller (more wetting) contact angle $\theta_1 = 75^\circ$.
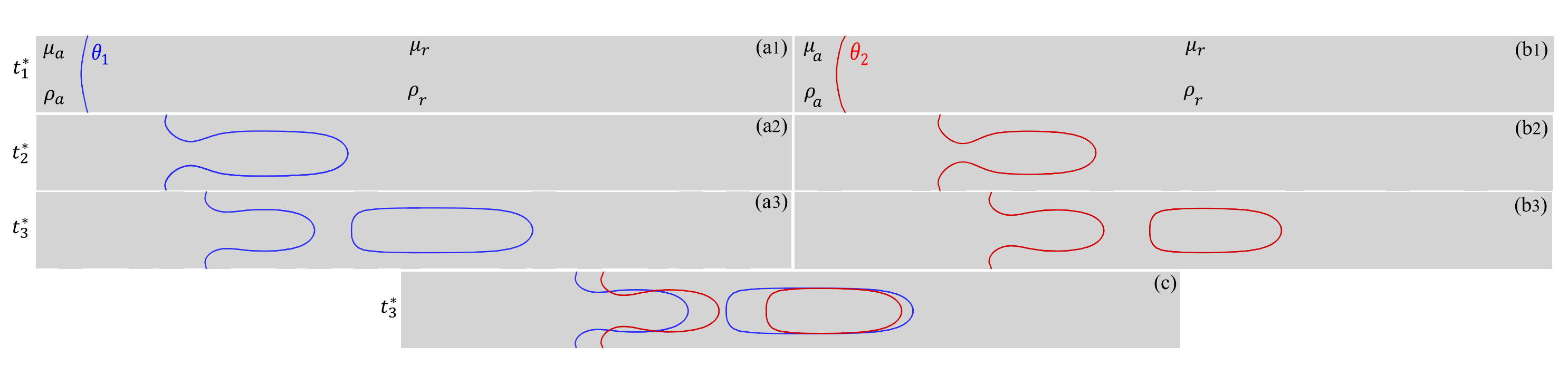Fig.5. Plots (a1) to (a3) and (b1) to (b3) show the interfacial evolution at three different time frames, $t^*_1$ to $t^*_3$, respectively for two non-wetting contact angles, $\theta_2 = 115^\circ > \theta_1 = 105^\circ$. For both contact angles, the capillary number ($\text{Ca}$) is the same, and above their corresponding critical contact line capillary numbers. ($\mu_a, \rho_a)$, $(\mu_r, \rho_r)$ are dynamic viscosity and density of the advancing and receding phases, respectively. Plot (c) compares the interfaces for contact angles $\theta_1 = 105^\circ$ and $\theta_2 = 115^\circ$ at the time frame $t^*_3$ shown in plots (a3) and (b3), where the interface corresponding to the contact angle $\theta_2 = 115^\circ$ is ahead of the interface corresponding to the smaller (more wetting) contact angle $\theta_1 = 105^\circ$.
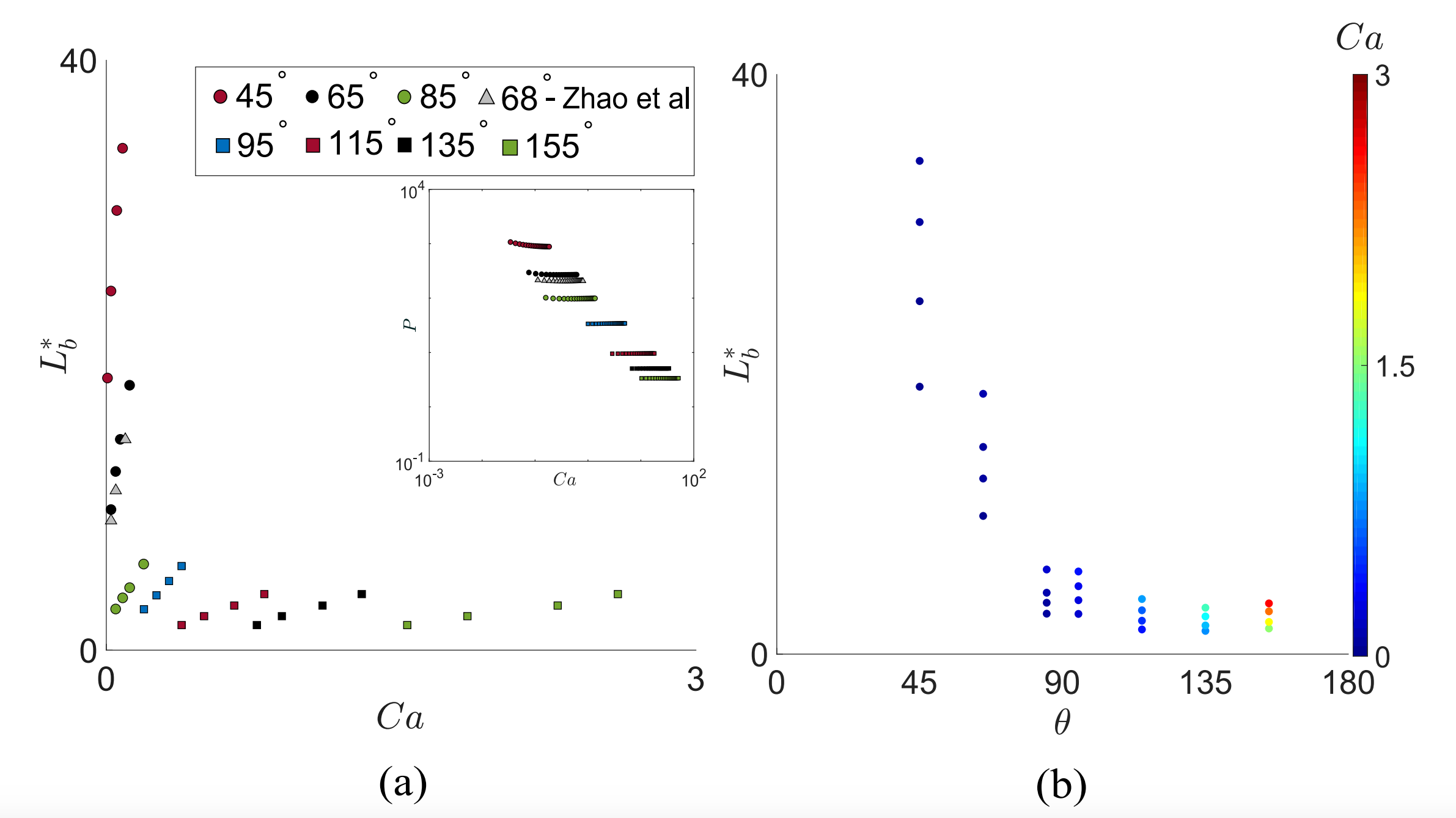Fig.6. (a) Illustration of the dimensionless blob length ($L^*_b = R^{-1}L_b$) as a function of the capillary number ($\text{Ca}$) for different wettability conditions, ranging from wetting ($\theta$ $<$ $90^\circ$) to non-wetting ($\theta$ $>$ $90^\circ$) contact angles. $L_b$ is the blob length and $R$ is the tube radius. The values for $\theta = 68^\circ$ correspond to the experimental data of Zhao et al.. The inset shows $P$ vs. $\text{Ca}$ where $P$ is a measure of the sensitivity of $L^*_b$ to $\text{Ca}$ and defined as $P=d\,\mathscr{L}/d\,\text{Ca}$. $\mathscr{L}$ indicates the dependence of the blob length on flow parameters and is defined as $\mathscr{L}=(h/R)^{-1}(\text{Ca}_f/\text{Ca}^{*}-1)$ where $h$ is the thickness of the receding phase layer left on the wall and $\text{Ca}_f = \text{Ca}/(1-h/R)^2$ is the finger capillary number. (b) Illustration of the dimensionless blob length as a function of the contact angle.
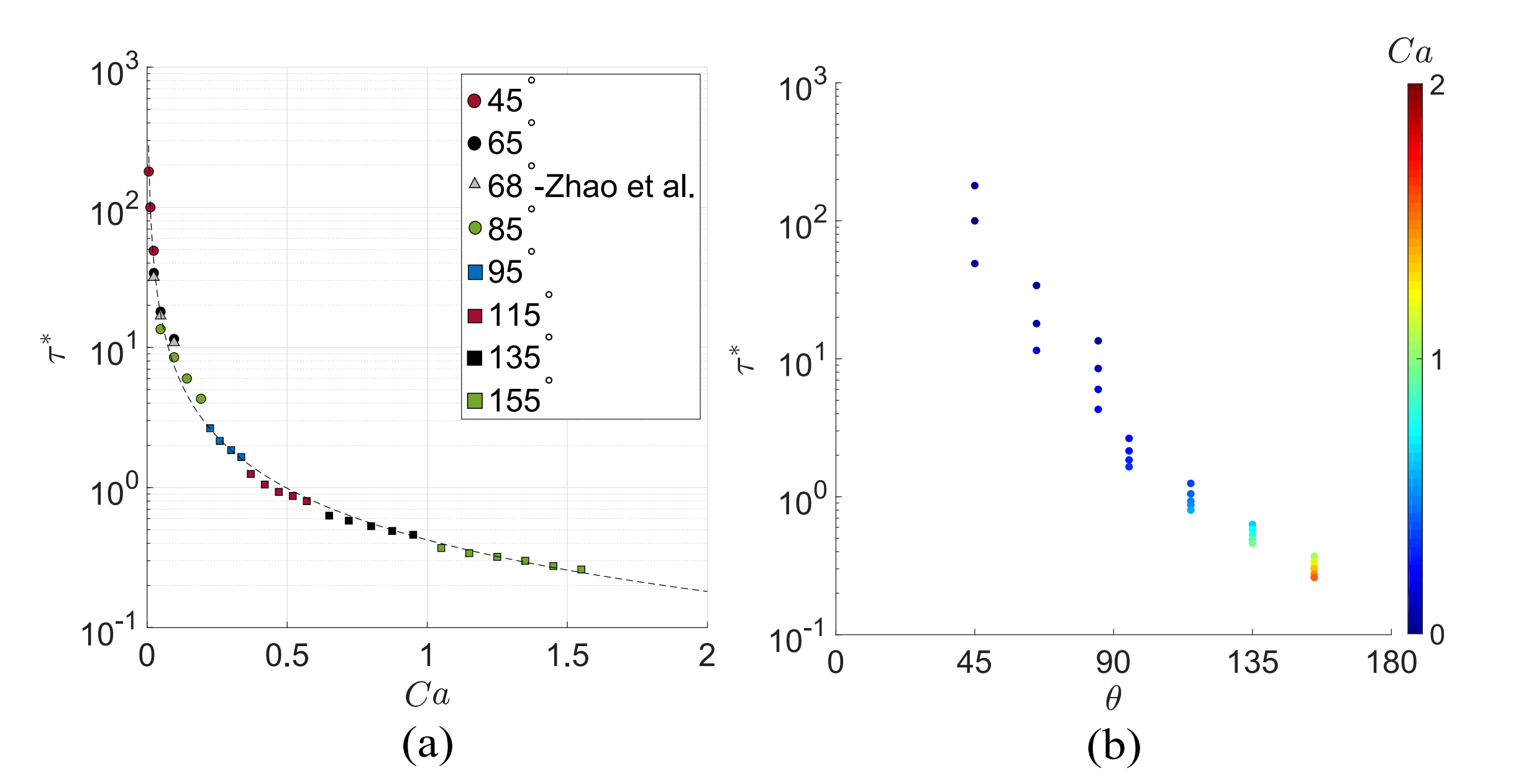Fig.7. (a) Illustration of the dimensionless pinch-off period ($\tau^* = \tau/t_c$) as a function of the capillary number ($\text{Ca}$) for different wettability conditions, ranging from wetting ($\theta$ $<$ $90^\circ$) to non-wetting ($\theta$ $>$ $90^\circ$) contact angles. $\tau$ is the time between two consecutive pinch-off events. Dashed curve is characterized by $\tau^* = 0.42\,\text{Ca}^{-1.2}$ which fits the dimensionless pinch-off period points with a regression coefficient of determination ($R^2$ value) of 0.998. The values for $\theta = 68^\circ$ correspond to the experimental data of Zhao et al. (b) Illustration of the dimensionless pinch-off period as a function of the contact angle.
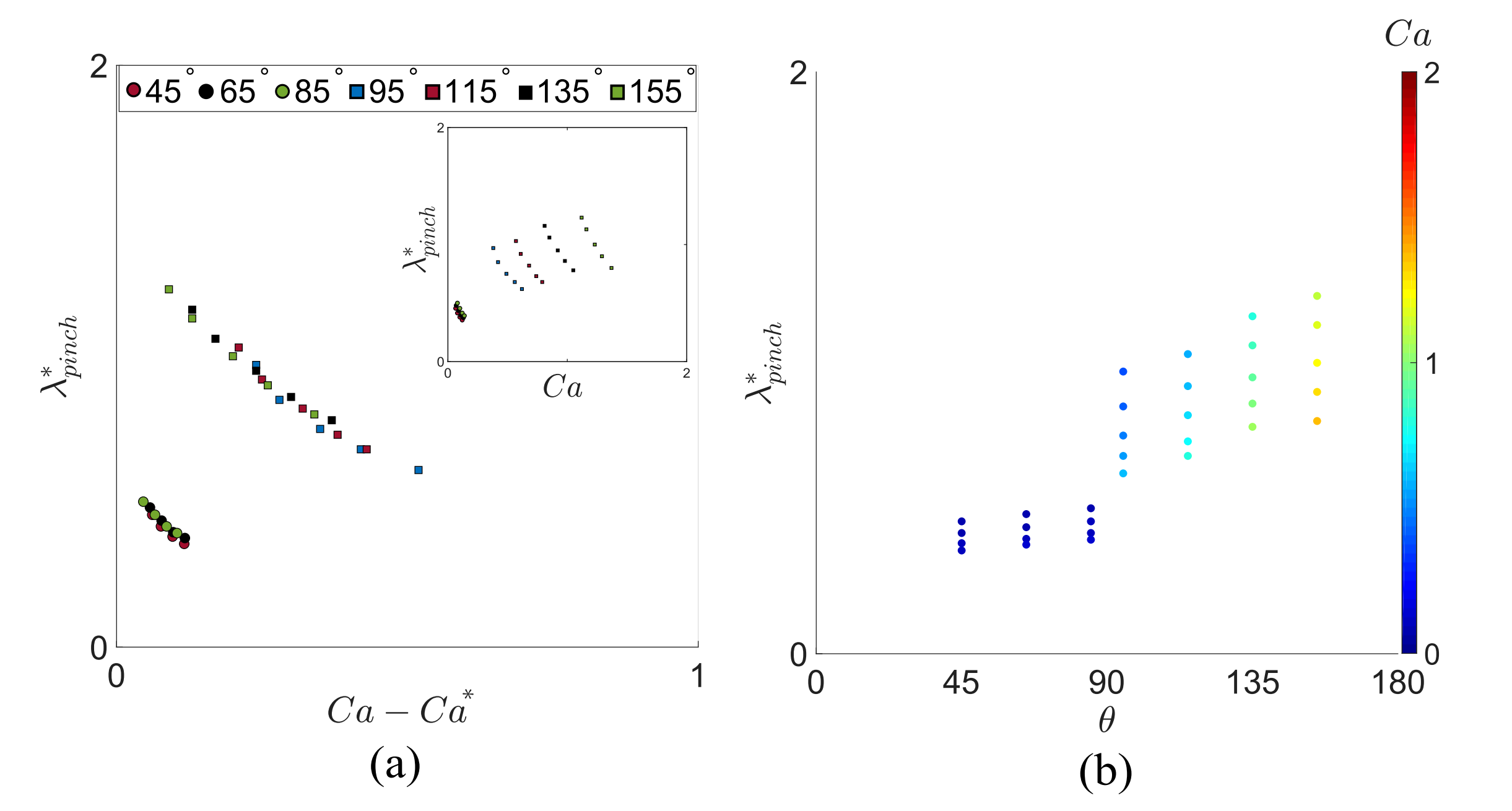Fig.8. (a) Illustration of the dimensionless blob separation distance ($\lambda^*_{pinch} = D^{-1}\lambda_{pinch}$) as a function of the difference between the capillary number ($\text{Ca}$) and the critical value of the contact line capillary number ($\text{Ca}^*$) for different wettability conditions, ranging from wetting ($\theta$ $<$ $90^\circ$) to non-wetting ($\theta$ $>$ $90^\circ$) contact angles. $\lambda_{pinch}$ is the blob separation distance and $D$ is the capillary tube diameter. The inset shows $\lambda^*_{pinch}$ as a function of the injection capillary number ($\text{Ca}$). (b) Illustration of $\lambda^*_{pinch}$ as a function of the contact angle.
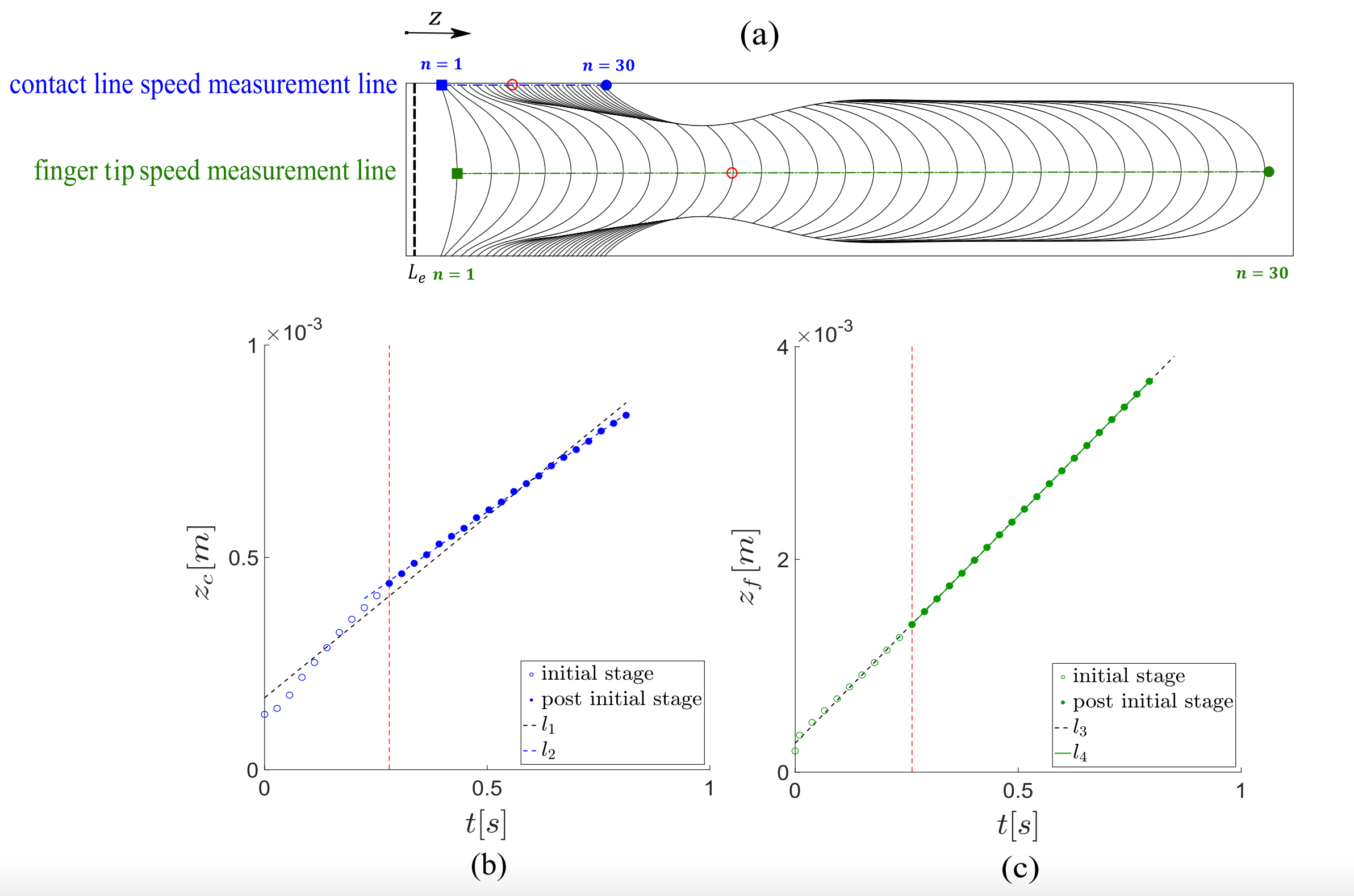Fig.9. Plot (a) shows the interface at 30 time frames captured evenly in time for an injection capillary number of $\text{Ca}= 0.0475$ and the contact angle of $\theta = 68^\circ$. $n=1$ and $n=30$ correspond to the initial and final time frames, respectively. In plot (a), the dashed blue and green lines respectively illustrate the direction along which the velocity of the contact line and finger tip are measured. The dashed black line ($L_e$) marks the size of the entry length. $z_c$ and $z_f$ respectively are the axial location of the contact line and the finger tip and $t$ is the physical time. The dashed red line separates the initial stage (i.e., before contact line reaches its critical speed) from the post-initial stage (i.e., after contact line reaches its critical speed).
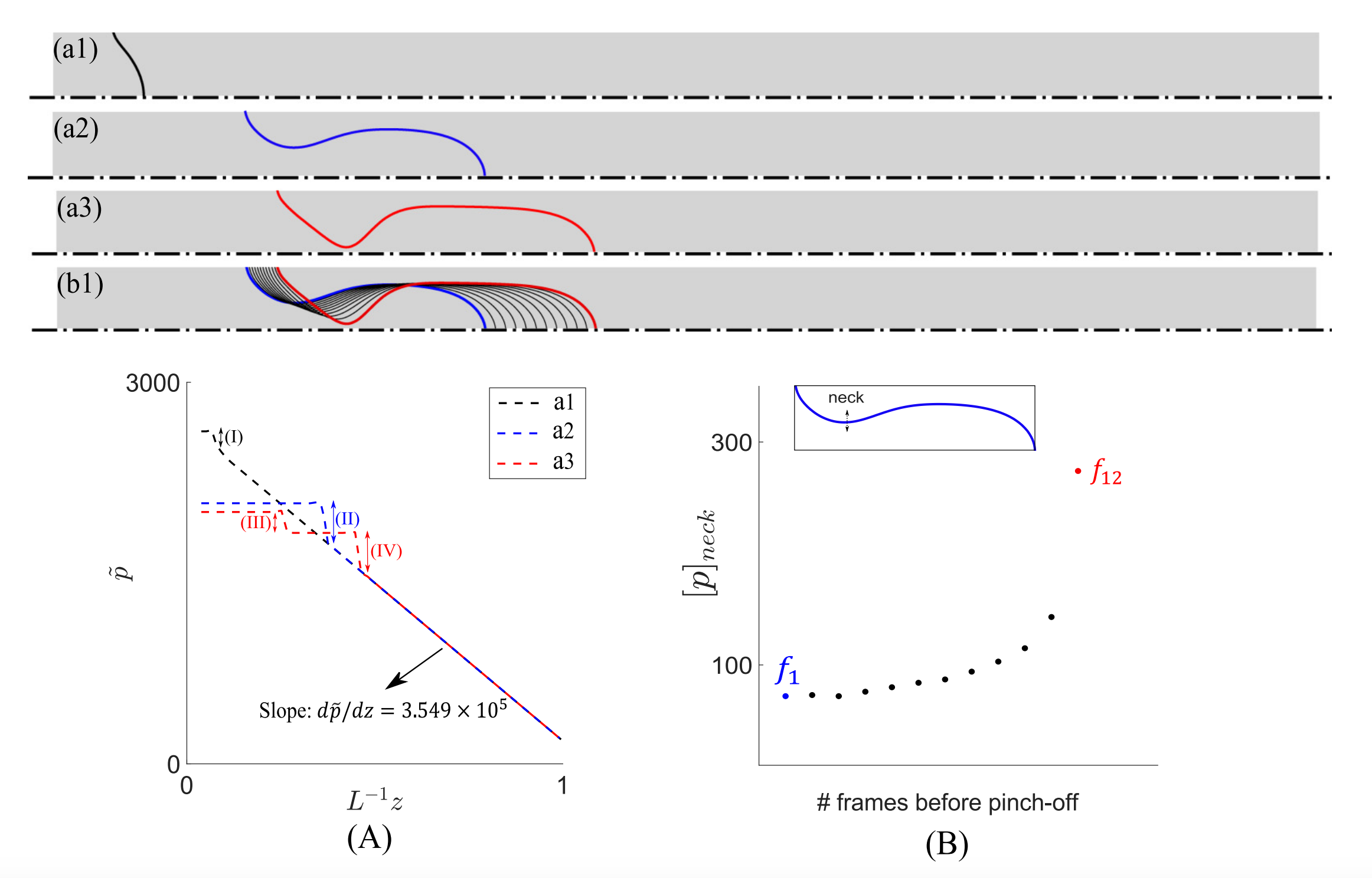Fig.10. Plots (a1) to (a3) respectively show the interface configuration in the beginning, prior to pinch-off, and at pinch-off for a contact angle of $\theta = 85^\circ$. Plot (A) shows the pressure difference with respect to the outlet pressure ($p_0$) measured along the axis of symmetry ($\tilde{p} = p_{(r=0,z)}-p_0$) for interfacial configurations presented in plots (a1) to (a3). For plot (a1) the pressure jump [$\,\tilde{p}\,$]$_\text{(I)}$ happens due to the curvature induced surface tension forces across the interface ($\sigma\kappa$), and is smaller than the jump in plot (a2) ([$\,\tilde{p}\,$]$_\text{(II)}$) due to a smaller interface curvature. In plot (a3) we observe two jumps in $\tilde{p}$, first one occurs at the necking position where pinch-off is about to happen and the second one occurs at the finger tip. The slope of the linear part of $\tilde{p}$ curves vs. $z$ follows the Darcy-Weisbach expression (${d \tilde{p}}/{dz}={128\,\mu Q}/{(\pi D^{4})}$) for laminar pipe flows which gives ${d \tilde{p}}/{d z} = 3.55\times10^5$ for glycerol occupying the capillary tube beyond the finger front. Plot (B) shows the pressure jump in the radial direction across the trailing neck of the growing finger ([$\,p\,$]$_\text{neck}$) for 12 equally spaced time frames ($f_1$ corresponds to plot (a2) and $f_{12}$ corresponds to plot (a3)). As the interfacial dynamics evolve toward pinch-off, the [$\,p\,$]$_\text{neck}$ increases and at the time of pinch-off suddenly accelerates and undergoes a jump.
