Two-phase Multiscale Numerical Framework for Modeling Thin-films on Curved Solid Surfaces in Porous Media

Authors - Zhipeng Qin, Soheil Esmaeilzadeh, Amir Riaz, and Hamdi A. Tchelepi

Download the Journal Version

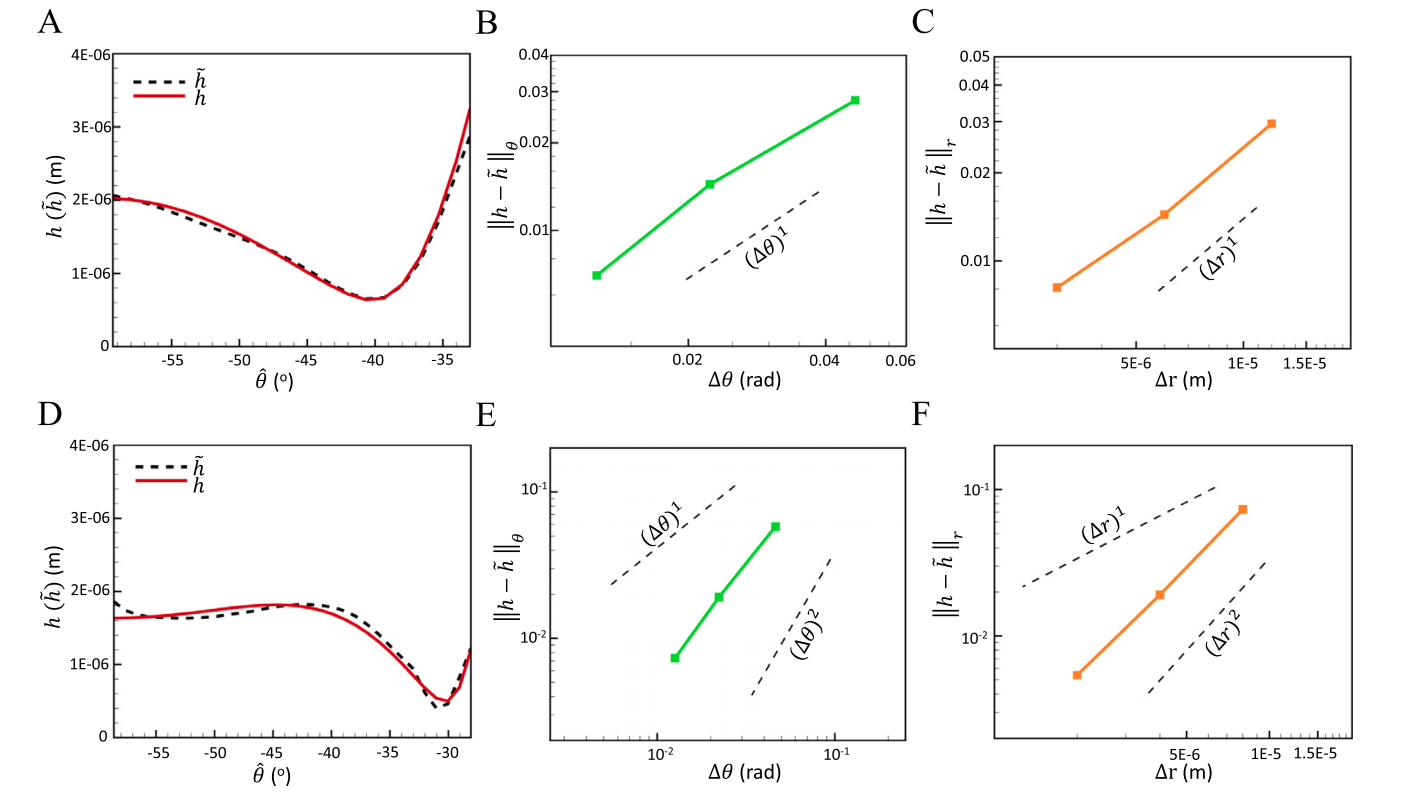
Abstract - Complex solid geometries, subgrid thin films, and interfacial deformations are critical for studying multiphase flows in porous media. However, it is challenging to accurately predict the flow evolution in porous media because of the difficulties in capturing the fluid-solid and fluid-fluid interactions in complex-shaped confinements at the pore-scale. In this work, we propose a multiscale continuum framework enabling the accurate simulation of the multiphase flow physics in complex porous media. Within this framework, we couple an efficient and accurate incompressible Navier-Stokes solver developed on a fixed Cartesian grid with a level-set method designed for capturing the interface between immiscible two-phase flows at low Capillary numbers. To capture the effects of complex solid boundaries on the flow dynamics, we employ an immersed boundary method based on a direct forcing approach. Most importantly, we develop a subgrid-scale thin-film model on a cylindrical coordinate around the curved solid surfaces to resolve the thin liquid films below the grid resolution and capture their effects on the fluid-fluid interfaces. The proposed multiscale framework illustrates how the embedded subroutines such as the level-set approach, the immersed boundary method, and the thin-film model can be coupled in order to capture the crucial physics involved in multiphase flow within porous media at different length scales.

Keywords: Multiphase flow, Porous media, Immersed boundary method, Level-set method, Thin films, Curved solid surfaces

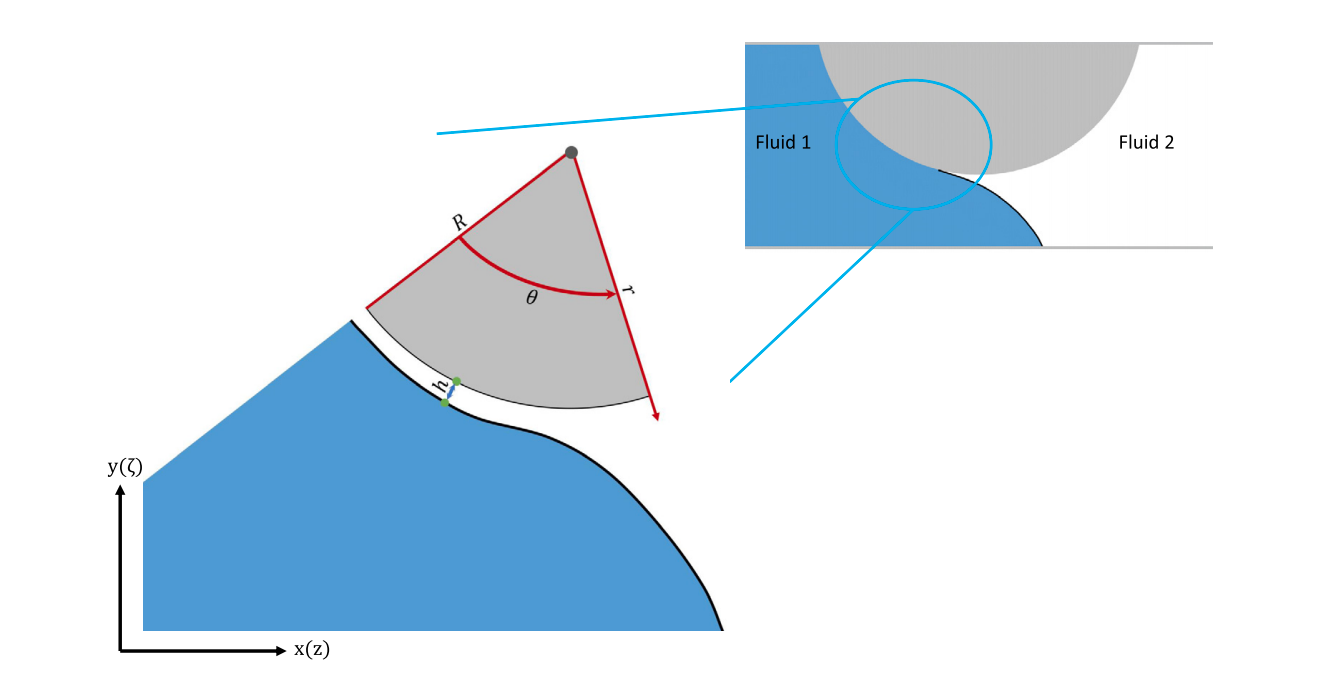
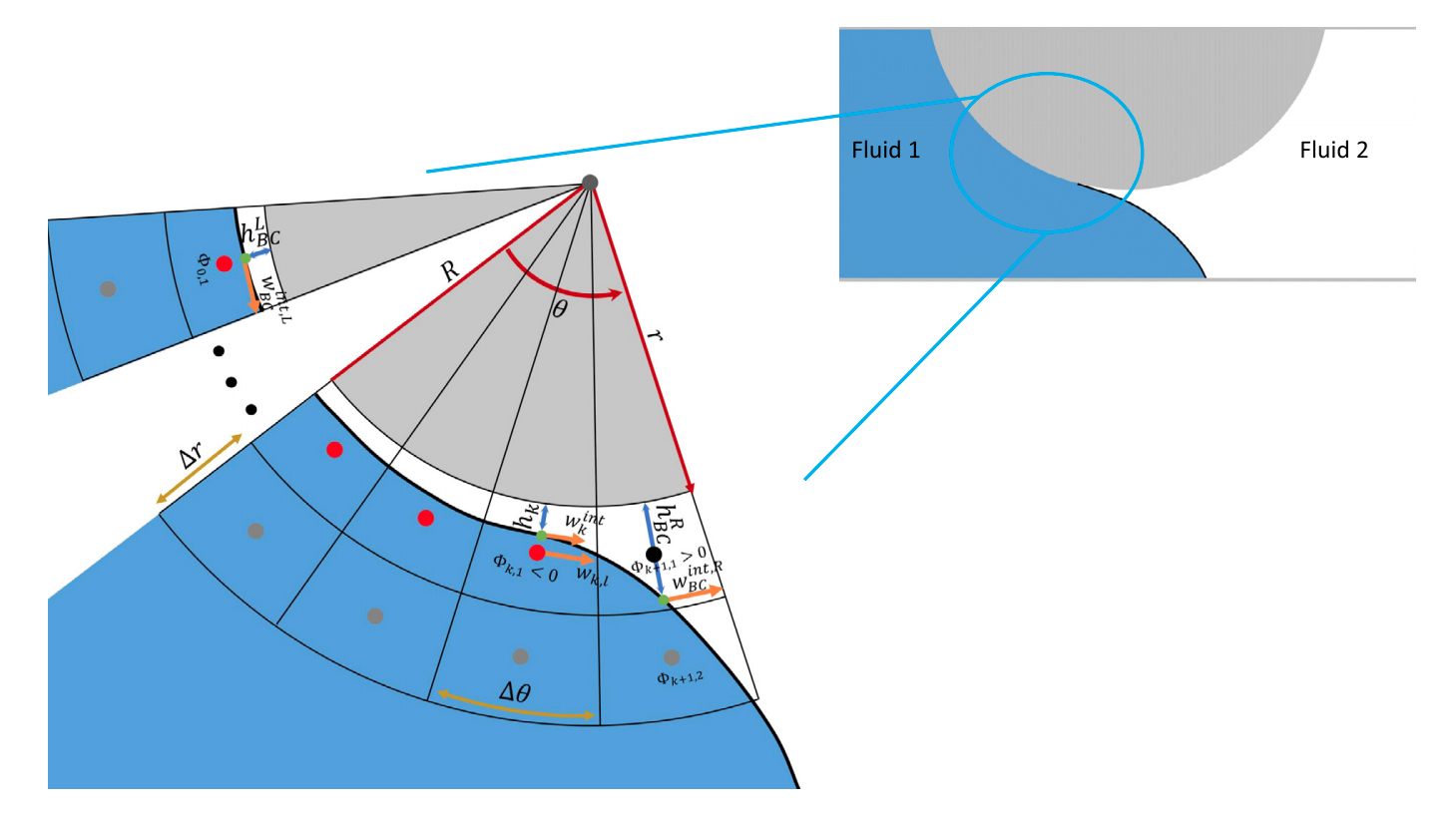
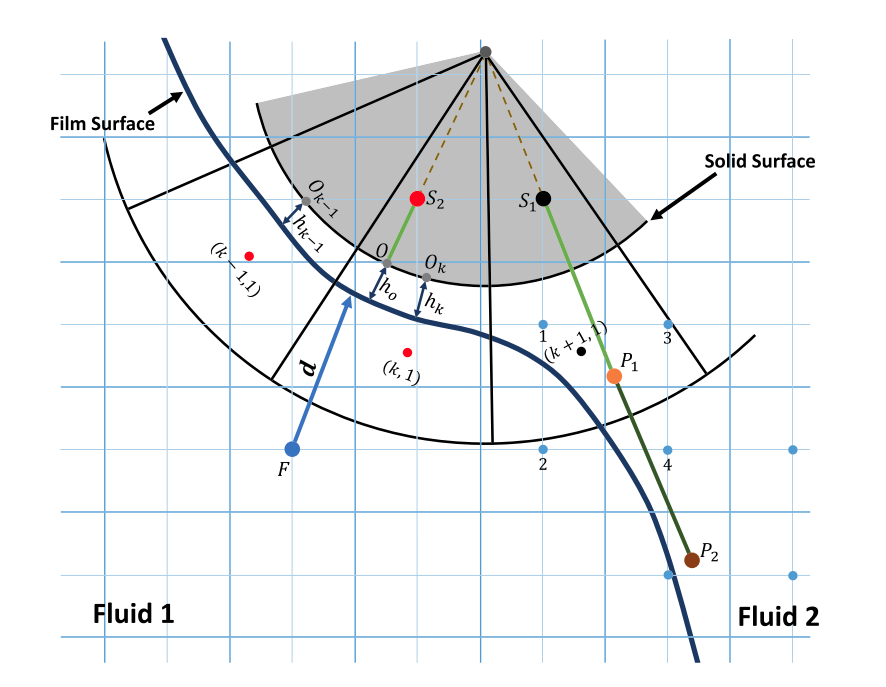
Fig.1. Zoomed in meniscus profile around a spherically curved surface, illustrating the computation of the thin-film thickness, $h$, based on multiscale coupling $r−\theta$ cylindrical coordinates and $x−y$ Cartesian coordinates or $z-\zeta$ axisymmetric coordinates.

Fig.2. Zoomed in meniscus profile around a curved solid surface in the cylindrical coordinate system. Here we illustrate the components for computation of the thin-film thickness based on the cylindrical coordinate system.

Fig.3. Schematic description of our level-set method. We define the boundary conditions for the advection of the level-set function by extrapolating the level-set value from the fluid domain to the solid domain, e.g., from points $P_1$ and $P_2$ to point $S_1$ or from the corresponding thin film to point $S_2$. For mass conservation, we employ a topological preserved reinitialization strategy to keep the level-set function in the fluid domain, e.g., at grid-cell $F$ , as a signed distance function.

Fig.4. $A$ and $D$ respectively compare the thickness of subgrid 2D and 2D-axisymmetric thin film, $h$, captured by the proposed multiscale model, to that of the fully resolved thin film, $\tilde{h}$; $B$ and $E$ present a convergence study in $\theta$-component for the L2 error of thin-film thickness, for the 2D and 2D-axisymmetric cases, respectively; Similarly, $C$ and $F$ present a convergence study in $r$-component for the L2 error of thin-film thickness.