

Authors - Soheil Esmaeilzadeh and Mohammad-Reza Alam
Download the Journal Version Download the arXiv Version
Abstract - Here, through a systematic methodology and the use of high performance computing, we calculate the optimum shape for a wave energy converter under the action of incident waves of (i) monochromatic unidirectional, (ii) monochromatic directional, (iii) polychromatic unidirectional, and (iv) polychromatic directional (with both directional symmetry and asymmetry). As a benchmark for our study, without loss of generality, we consider a submerged planar pressure differential wave energy converter, and use Genetic Algorithm to search through a wide range of shapes. A new parametric description of absorber shape based on Fourier decomposition of geometrical shapes is introduced, and for each shape hydrodynamic coefficients are calculated, optimum power take-off parameters are obtained, and overall efficiency is determined. We show that an optimum geometry of the absorber plate can absorb a significantly higher energy (in some cases a few times higher) when compared to a circular shape of the same area. Specifically, for a unidirectional incident wave, the optimum shape, as expected, is obtained to be the most elongated shape. For directional incident waves, a butterfly-shape is the optimum geometry whose details depend on not only the amplitude and direction of incident wave components, but also the relative phases of those components. For the latter effect, we find an optimally averaged profile through a statistical analysis.
Keywords: Shape Optimization, Hyperformance Computing, Numerical Modeling, Wave Energy Converter, Directional Incident Wave
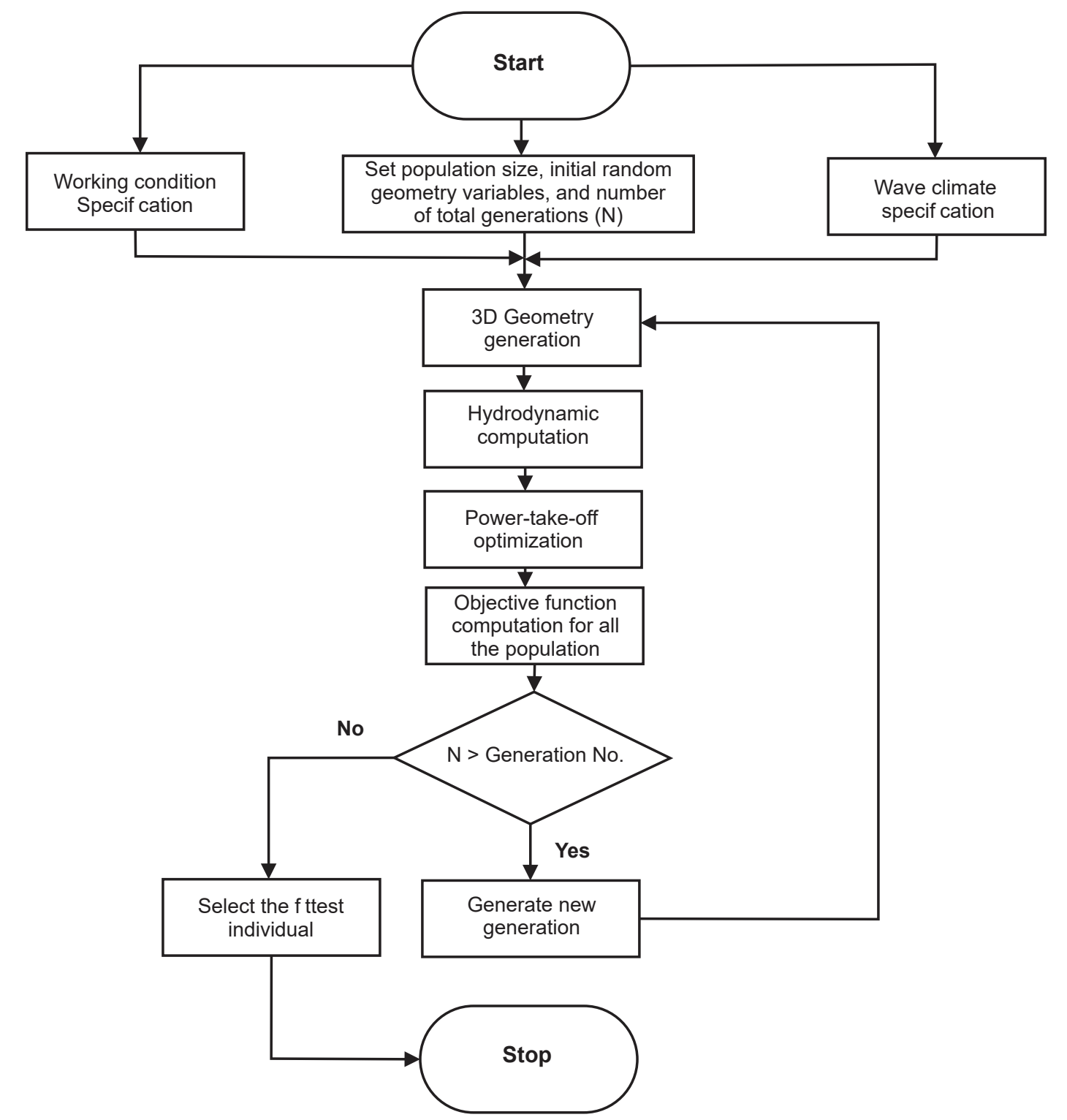
Fig.3. Flowchart of shape optimization process. We start by specifying the working conditions of the device e.g. operating depth, sea bottom depth and incident spectrum, as well as Genetic Algorithm (GA) parameters. Next, by using our shape generation method, shapes are generated and meshed. Then through Boundary Element Method (BEM) solver NEMOH, hydrodynamic coefficients of each shape are calculated. Next, the optimum power take-off parameters for each shape are found using a separate optimization subroutine. At the next step, the objective function value, i.e. the power that can be absorbed by each shape, is calculated. Then the evolutionary process of GA optimization continues until reaching to the maximum number of generations where the optimization process stops and the shape with maximum absorbed power is chosen as the optimum shape. For each optimization case the maximum number of generations is tuned in a way that the increment in absorbed power by the fittest individual in the consecutive generations be small and when there is no significant improvement in the values of fitness of the population from one generation to the next. On average an optimization case for a broadband directional wave climate required $21.71$ hours of computation on $8$ CPU cores.
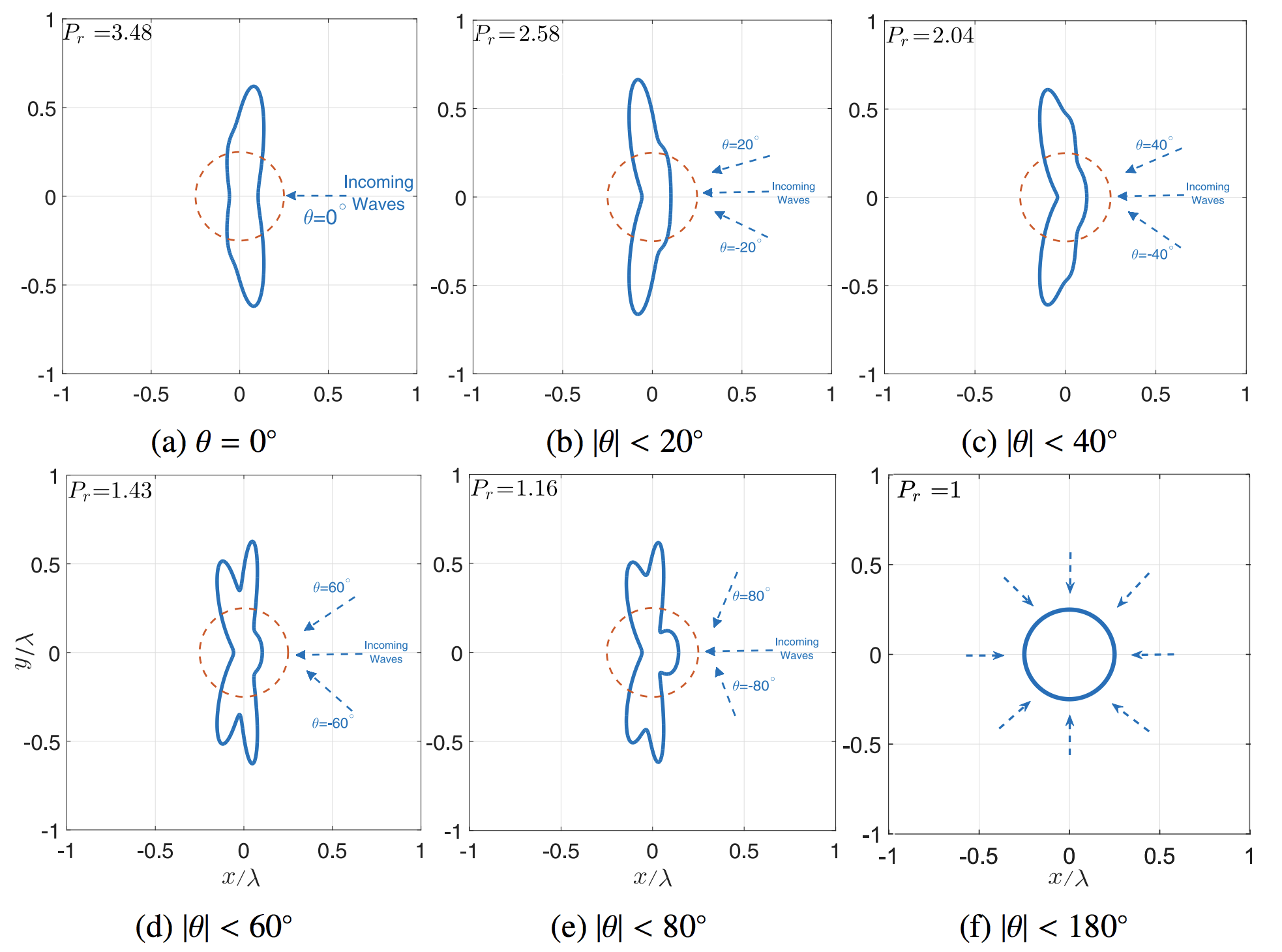
Fig.4. Optimum absorber plate’s shapes for monochromatic directional incident waves whose energy is uniformly distributed across the provided range of $\theta$. As the spreading angle increases from $\theta = 0^\circ$, the optimum shape leans symmetrically backward to face maximum area of itself normal to the incident wave energy. With a further increase in the directorial range, i.e. for |$\theta$| $<60^\circ$, $80^\circ$, a double-wing topology is obtained, as well as a bulge-shaped area in the middle that captures energy of high-angle incident waves. In the limit of |$\theta$| $<180^\circ$, the optimum shape is a circle. Coefficients of shape generation Fourier modes are given in the paper.